編碼器概觀

輸入序列被 embedding 及加上位置編碼後，下一步即是將其匯入編碼器的第一層，接著第二層，最後到第六層輸出。因為編碼器的每一層結構都是相同的，所以我們了解第一層的處理方式即可，其他層的處理程序都是相同的。

下圖（註一）是一個簡化的編碼器，它的輸入序列只有兩個元素 (Xi)，經過 Self-Attention 子層 (正式的名稱是 Multi-Head Attention) 後，會輸出 Zi，注意的是，每一個輸入元素 Xi 會輸出對應的 Zi，它們的大小都是 512 。各個 Zi 「分別」輸入「同一個」Feed Forward Neural Network (FFNN)，產生 ri 為第一層的輸出，可作為第二層的輸入。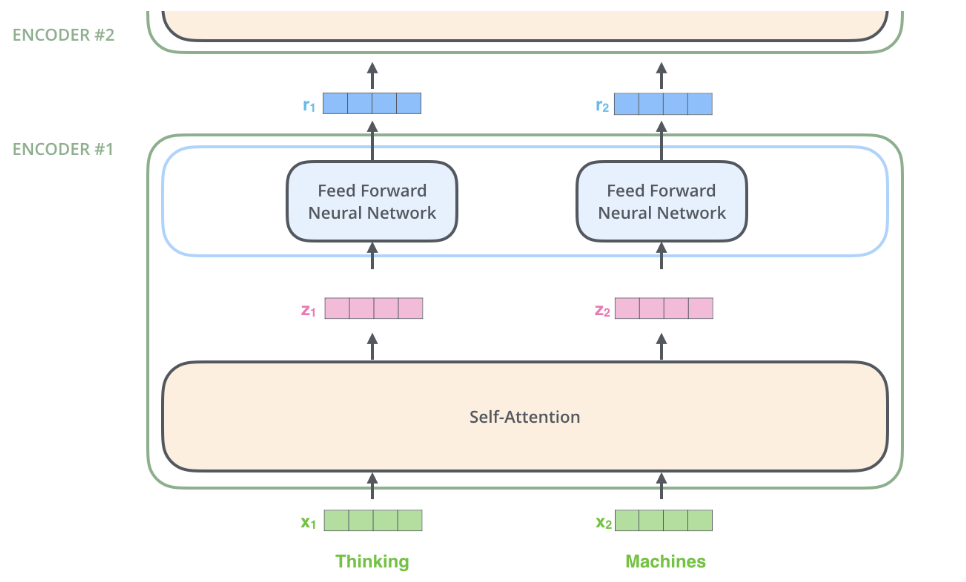

為了強調每個 Zi 是分別輸入 FFNN 的，所以上圖將 FFNN 畫了兩次，事實上它們是同一個 FFNN。這種設計就是所謂的 Positionwise Fully Connected Feed-Forward。

Transformer 使用了非常簡單的 FFNN，它僅有兩個 linear 層，並且使用 ReLu 做為其 Activation Function。

Multi-Head Attention　概觀

Transformer 所用的 Attention 機制，正確的說，是使用基於「Self-Attention」的「Scaled Dot-Product Attention」，並在同一個子層中，使用 8 個平行的 「Scaled Dot-Product Attention」，成為「Multi-Head」Attention 結構。聽起來很饒舌，接下來老頭就分別解析它的意思。在下文中老頭大量參考了《The Illustrated Transformer》(註一）中的素材，在此向 Jay Alammar 致謝，發表了那麼好的文章。

下圖是 Multi-Head Attention 和 Scaled Dot-Product Attention 的示意圖：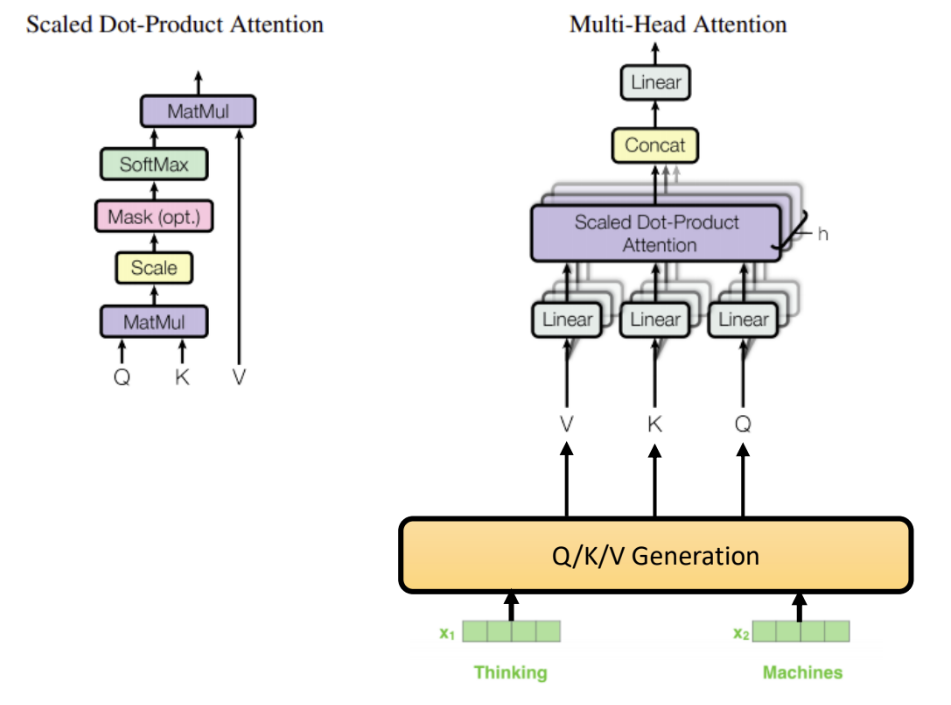

圖的右下表示輸入序列，對於編碼器的第一層而言，它們是經過 Embedding 和位置編碼的的輸入序列，對於編碼器的第二層以上的各層而言，它們是前一層的輸出。

接下來，經過 Q/K/V Generation 運算，每一個輸入的元素，對每一個 Scaled Dot-Product Attention，皆會產生其對應的 Q 向量、 K 向量、及 V 向量！也就是說，假設輸入序列有 n 個元素，一層有 h 個 Scaled Dot-Product Attention，那麼 Q/K/V Generation 將需產生 n x h 組 (Q, K, V) 向量。

由同一個輸入序列，產生出 (Q, K, V) 的這個動作，就是 Self-Attention。(這是一個相當不完整的定義，希望未來能有機會好好的把 Attention 說明清楚）

(Q, K, V) 產生之後，分別將它們交給對應的 Scaled Dot-Product Attention 處理，出來的 h 份結果（預設是 8) 經過一個 Linear 層將其降維度，即可成為下一個子層 (FFNN) 的輸入。對於 FFNN 子層而言，它的輸入即是一個 Scaled Dot-Product Attention 子層的輸出，所以 h 份結果必須降維成一份結果的維度，才能成為 FFNN 的輸入。

Q, K, V 的生成

下圖（註一）表示了針對某一個 Scaled Dot-Product Attention 產生 Q, K, V 的圖示：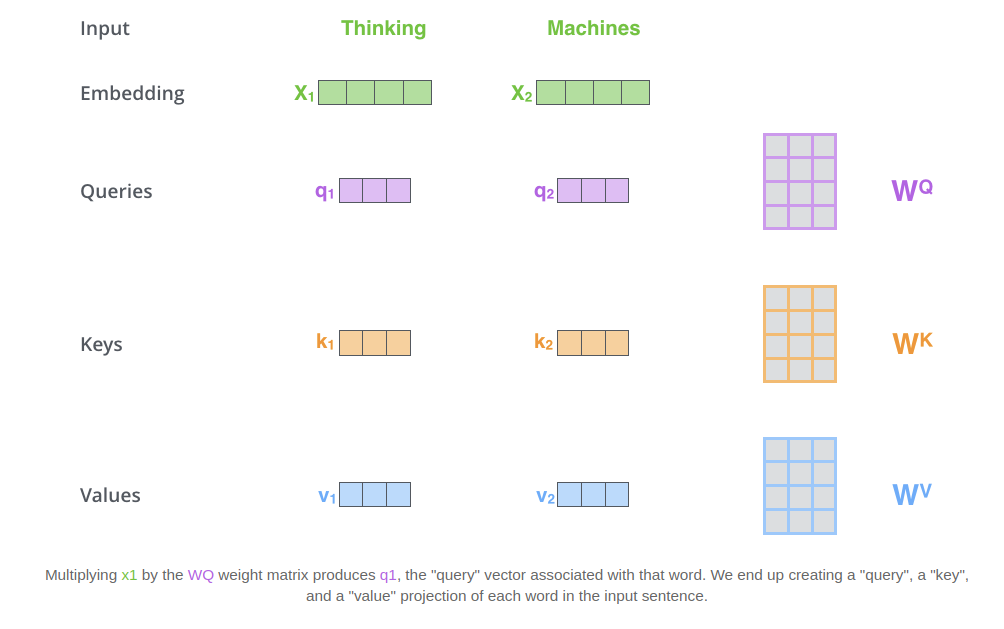

每一個 Scaled Dot-Product Attention 有一組屬於它自己的權重矩陣 (WQ, WK, WV)，輸入 Xi 和 WQ 作矩陣相乘，即得 qi，以此類推，算出各個輸入的對應 q/k/v。

X1 x WQ = q1
X1 x WK = k1
X1 x WV = v1

X2 x WQ = q1
X2 x WK = k2
X2 x WV = v2

（註一：源自 Jay Alammar 的《The Illustrated Transformer》 ）